Without a doubt, the most beautiful ornament to put at the top of a Christmas tree is a stellated dodecahedron. It is of upmost importance to CoolGear's bottom line to develop the most efficient possible process to manufacture these ornaments. 

But let's not get too far ahead ourselves -- before we can make stellated dodecahedrons, we first need to nail down the best way to make simple dodecahedrons. 

One easy way to mass-produce dodecahedrons is to cut out a flat unfolded shape from cardboard, and then fold it into a dodecahedron.

Problem 1
How many unique ways are there to unfold a dodecahedron onto a flat surface so that all of the faces stay connected and do not overlap? Reflected and rotated versions of unfoldings do not contribute to the total count.

Here is an example of one possible way to unfold a dodecahedron:



For reference, if we were considering tetrahedrons, rather than dodecahedrons, the answer would be 2.
Similarly, if we were considering cubes, the answer would be 11.
 

Problem 2
Suppose that one edge of a dodecahedron has a length of 1. 

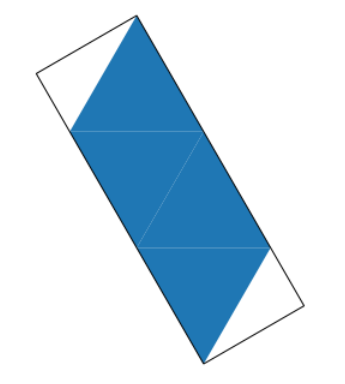
We want to find the smallest bounding rectangle, i.e. the unfolding of a dodecahedron that can be cut out of the smallest possible rectangular sheet of cardboard.

For reference, the smallest bounding rectangle for a tetrahedron has an area of 5*sqrt(3)/4 ≈ 2.165:



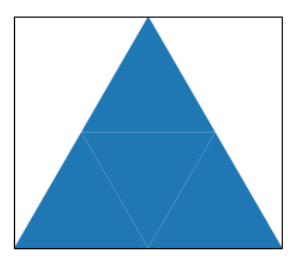
We also want to find the largest bounding rectangle, i.e. the unfolding of a dodecahedron that requires the largest possible rectangular sheet of cardboard.

For reference, the largest bounding rectangle for a tetrahedron has an area of 2*sqrt(3) ≈ 3.464:



What is the difference in area between the smallest and largest bounding rectangles for a dodecahedron? (Round your answer to three decimal places.)

For reference, the answer would be 1.299 if we were considering tetrahedrons, rather than dodecahedrons.